• zobacz księgę

• LICYTACJA
• WIST
• ROZGRYWKA
• ZAPIS
• KONWENCJE
• MATERIAŁY

Rozgrywka

Prawdopodobieństwo

Wiadomości ogólne

Zapewne nikt nie będzie robił wyliczeń przy stoliku, elementarna wiedza jest potrzebna natomiast choćby do porozdaniowej analizy. Będzie trochę wzorów i matematyki niestety.

Generalnie prawdopodobieństwo wystąpienia jakiegoś zdarzenia A jest to stosunek liczby układów sprzyjających do liczby wszystkich układów. Układy sprzyjające to takie, przy których odniesiemy sukces - na przykład król pod impasem.

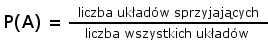
Powyższa definicja w praktyce jest przydatna do obliczenia prawdopodobieństwa z niewielką liczbą układów. Dla układu impasowego AD10 mamy cztery możliwości:

• król u W
• walet u W
• obie figury u W
• obie figury u E

Jeśli interesuje nas wzięcie trzech lew - to układ sprzyjający jest tylko jeden (obie figury u W). Prawdopodobieństwo sukcesu więc to 1/4 czyli 25%

Jeśli interesuje nas zdarzenie odwrotne to prawdopodobieństwo możemy obliczyć odejmując wynik od 1, gdyż suma prawdopodobieństw dla wszystkich możliwości tyle właśnie wynosi. Dla powyższego przykładu zdarzeniem odwrotnym jest nieudanie się choć jednego impasu. Prawdopodobieństwo tego wynosi: 1 - 1/4 = 3/4 czyli 75%.

Gdy rozpatrujemy kilka zdarzeń łącznie do obliczania prawdopodobieństwa stosujemy kilka wzorów:

Iloczyn prawdopodobieństw

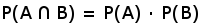
Wzór odnosi się do przypadku jednoczesnego zajścia dwóch zdarzeń, czyli do przypadku, kiedy musi zajść jedno i drugie zdarzenie. Oba zdarzenia muszą być ponadto niezależne czyli zajście jednego zdarzenia nie rzutuje na drugie.

W przykładzie na początku mieliśmy możliwość zastosowania tego wzoru.

• Zdarzenie A - walet pod impasem, prawdopodobieństwo 50%, bo walet może być albo u W albo u E
• Zdarzenie B - król pod impasem, prawdopodobieństwo również 50%

Nas interesowało łączne wystąpienie obu zdarzeń, czyli walet i król u W - prawdopodobieństwo tego to 50% * 50% czyli 25% .

Sposób obliczania prawdopodobieństwa zdarzeń zależnych jest nieco trudniejszy - zostanie omówiony w następnym rozdziale.

Suma prawdobieństw

Z sumą prawdopodobieństw mamy do czynienia wszędzie tam, gdzie gdzie ma wystąpić jedno lub drugie zdarzenie. W początkowym przykładzie byłoby to udanie się chociaż jednego impasu.

Do obliczenia sumy stosuje się jeden z dwóch wzorów:

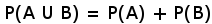
Czyli normalne dodawanie prawdopodobieństw. Tak postąpić możemy tylko wtedy gdy zdarzenia się wzajemnie wykluczają. Na przykład mając w kolorze 7 kart, gdy interesuje nas podział nie gorszy niż 4-2, czyli 4-2 lub 3-3, prawdopodobieństwo możemy obliczymy dodając prawdopodobieństwa jednego i drugiego podziału: 48% + 36% = 84%

Jeśli jedno zdarzenie nie wyklucza drugiego to stosujemy inny wzór:

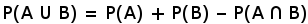
Od sumy obu prawdopodobieństw odejmujemy część wspólną. Wracając do początkowego przykładu:

• Zdarzenie A - walet pod impasem (50%)
• Zdarzenie B - król pod impasem (50%)
• Część wspólna obu zdarzeń czyli jednoczesne ich wystąpienie - to walet i król pod impasem (25%)

Prawdopodobieństwo króla lub waleta pod impasem to: 50% + 50% - 25% = 75%

Powyższe wzory pozwalają obliczyć prawdopodobieństwo wystąpienia dwóch zdarzeń w różnych relacjach. Jeśli interesuje nas większa liczba zdarzeń, proponuję wykorzystać do obliczeń sposób graficzny:

Drzewko prawdopodobieństw

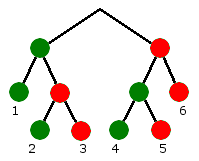
Poszczególne węzły diagramu obrazują sukces (kolor zielony) lub porażkę (kolor czerwony) jednego zagrania. Powyższy diagram odnosi się do takiedo zdarzenia: udanie się dwóch z trzech impasów. Każde rozgałęzienie oznacza impas z prawdopodobieńswem jednostkowym 50%. Idąc od góry:

• Pierwsze rozgałęzienie oznacza pierwszy impas, może on się udać bądź nie, stąd kropka zielona i czerwona
• Po wykonaniu pierwszego impasu, wykonujemy drugi - to środkowa sekcja diagramu
• Najniższe piętro oznacza trzeci impas. Jest trochę mniej "rozgałęzione", gdyż w dwóch przypadkach zdarzenie już zakończyło się sukcesem (wyszedł pierwszy i drugi impas) lub porażką (nie udał się ani pierwszy ani drugi impas). Te dwie sytuacje to odnogi oznaczone jako 1 i 6.

Po narysowaniu drzewka przystępujemy do obliczenia prawdopodobieństwa zdarzenia:

• Mnożymy prawdopodobieństwa jednostkowe w odnogach które zakończyły się sukcesem - czyli w naszym przypadku zawierają dwie zielone kropki.
  • Gałąź nr 1: 50% * 50% = 25%
  • Gałąź nr 2: 50% * 50% * 50% = 12,5%
  • Gałąź nr 4: 50% * 50% * 50% = 12,5%
• Dodajemy uzyskane wyniki. W naszym przykładzie: 25% + 12,5% + 12,5% = 50%

Poniżej jeszcze jeden przykład.

Załóżmy, że grasz kontrakt 6, po wiście atutowym i chcesz obliczyć prawdopodobieństwo wygrania. Jeśli w kolorze atutowym jest podział 2:2, to do wygrania kontraktu potrzebne jest albo udanie się impasu trefl, albo podział w karach 3:3. Jeśli atu się nie podzieli - to muszą podzielić się kara i musi stać impas króla. Drzewko prawdopodobieństw będzie wyglądało tak:

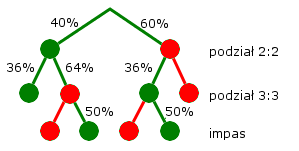
Prawdopodobieństwo wygrania szlemika: 40% * 36% + 40% * 64% * 50% + 60% * 36% * 50% =14,4% + 12,8% + 10,8% = 38%

© 2008 jafo