Rozgrywka
Prawdopodobieństwo
Kombinacje
W omawianych wcześniej przykładach liczba układów była na tyle mała, że można je było wszystkie wypisać i policzyć na palcach. Co jednak zrobić kiedy liczba możliwości jest duża? Można skorzystać z gotowych tabel, tak jak to już wcześniej zrobiliśmy, przyjmując na przykład w ostatnim przykładzie, że prawdopodobieństwo podziału 2:2 wynosi 40% (Tabela podziału koloru). Dla zainteresowanych w skrócie skąd takie liczby się wzięły.
W rachunku prawdopodobieństwa wykorzystywanych jest kilka wzorów w zależności od tego czy jest istotna kolejność elementów lub czy są możliwe powtórzenia. Jest to szeroko omówione choćby na www.math.edu.pl w dziale poświęconym kombinatoryce. Specyfika brydża jest taka, że nas interesuje praktycznie tylko jeden wzór dotyczący kombinacji
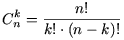
Wygląda groźnie jednak taki nie jest. Na początek co to za wykrzykniki. Jest to tzw silnia - działanie sprowadzające się do pomnożenia wszystkich liczb całkowitych od 1 do liczby przed wykrzyknikiem. Na przykład:
5! = 1 * 2 * 3 * 4 * 5 = 120
W przedstawionym wzorze są dwa parametry: n i k. Pierwszy z nich to liczba kart, z których tworzymy kombinacje, drugi mówi o tym ilu kartowe mają te kombinacje być. Dla zrozumienia sprawy prosty przykład. Jeśli mamy kolor dziewięciokartowy, podzielony u przeciwników 2:2, w którym brakuje A, K, 3 i 2 to jest możliwych sześć rozkładów (dla uproszczenia tylko jedna ręka): AK, A3, A2, K3, K2, 32. Korzystając z wzoru na kombinacje podstawiamy za n - liczbę brakujących kart czyli 4, a za k - 2, bo kombinacje mają być dwukartowe.
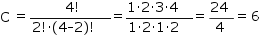
Jeśli komuś nadal wydaje się to za trudne to można skorzystać z tablic lub z kalkulatora. Najważniejsze aby dobrze określić n i k. Przejdźmy do konkretów.
Przykład 1 - prawdopodobieństwo podziału 3:3 u przeciwników jeśli mamy kolor 7-kartowy
- Ustalamy liczbę wszystkich możliwości. Do podziału między obrońców zostało 26 kart (n), każdy ma mieć po 13 kart (k). Pomijam proces obliczania tego - skorzystamy z kalkulatora. Liczba wszystkich kombinacji - 10 400 600.
- Ustalamy liczbę możliwych kombinacji dla badanego koloru. Brakuje 6 kart (n), kombinacje będą 3-kartowe (k), bo podział ma być 3:3. Możliwości jest 20
- Dodatkowo musimy uwzględnić rozkłady pozostałych 10 kart (k) w ręku obrońcy. Do rozdysponowania zostało jeszcze 20 kart (n), bo sześć już zostało rozdielonych. Liczba kombinacji - 184 756.
- Wszystkich układów sprzyjających jest więc 20 * 184 756 = 3 695 120
- Pozostało skorzystać z definicji prawdopodobieństwa: P = 3695120 : 10400600 = 35,53%
- Sprawdzamy w literaturze - zgadza się uff :-)
Gdyby była potrzeba obliczenia prawdopodobieństwa podziału 4:2. Trzeba by powyższą procedurę powtórzyć zarówno dla kombinacji 4-kartowych jak i 2-kartowych, a następnie dodać wyniki.
Przykład 2 - drugi król pod impasem, gdy mamy kolor 8-kartowy
- Liczba wszystkich możliwości to kombinacje 13-kartowe z 26 kart. Wynik jak wyżej.
- Poza królem brakuje 4 kart. Król ma być drugi, więc musi wystąpić z jedną z tych czterech. Są więc 4 możliwości.
- Sprawdzamy liczbę kombinacji dla 11 z 21 kart - 352 716
- Wszystkich układów sprzyjających jest więc 4 * 352 716 = 1 410 864
- P = 1 410 864 : 10 400 600 = 13,57%
Przykład 3 - DW sec za impasem przy kolorze 9-kartowym
- Liczba wszystkich możliwości to kombinacje 13-kartowe z 26 kart. Wynik jak wyżej.
- Skoro ma być DW bez blotek, więc jest tylko jeden taki układ
- Pozostałe karty utworzą kombinacje 11 elementowe, do rozdysponowania są 22 karty. Jest 705 432 możliwości.
- P = 705 432 : 10 400 600 = 6,78%
© 2008 jafo