• zobacz księgę

• LICYTACJA
• WIST
• ROZGRYWKA
• ZAPIS
• KONWENCJE
• MATERIAŁY

Rozgrywka

Prawdopodobieństwo

Prawdopodobieństwo warunkowe

Dotyczy ono zdarzeń zależnych. Jeśli wystąpienie jakiegoś zdarzenia powoduje zmianę prawdopodobieństwa wystąpienia innego, to są to właśnie zdarzenia zależne. Podczas rozgrywki takie sytuacje występują bardzo często. Jeśli na przykład w kolorze 7-kartowym jest do wykonania impas a wiadomo (z licytacji, wistu), że kolor ten podzielił się 4-2 to szansa na udanie się impasu zmienia się.

Prawdopodobieństwo warunkowe zapisuje się w taki sposób - P(A|B). Co oznacza, że chodzi o prawdopodobieństwo zdarzenia A pod warunkiem, że zaszło zdarzenie B. I wzór na takie prawdopodobieństwo:

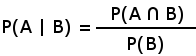
No to policzmy jaka jest szansa impasu króla u W jeśli wiadomo,że ma on cztery karty a E tylko dwie.

• A - król u W
• B - 4 karty u W. Prawdopodobieństwo odczytamy z tabeli podziału koloru. Z tym, że prawdopodobieństwo tam podane trzeba podzielić na pół, bo chodzi o tylko połowę podziałów 4:2, tą w której 4 karty są u W. P(B)=24%
• A∩B - część wspólna A i B czyli czwarty król u W. Prawdopodobieństwo można policzyć stosując kombinacje, dla ułatwienia skorzystamy z tabeli prawdopodobieństwa niektórych układów: prawdopodobieństwo czwartej figury przy brakujących 6 kartach wynosi - 16%
• A|B - król u W jeśli W ma 4 karty. Podstawiając do wzoru: P(A|B)=P(A∩B)/P(B)=16%/24%=67%

Jak widać znacznie wzrosły szanse impasu króla. Na "chłopski rozum" można do problemu było podejść tak: król u W wystąpi z 3 blotkami, jest więc 10 takich możliwości (kombinacje 3 blotek z pięciu), a u E tylko z jedną. Tych drugich układów jest tylko pięć. Prawdopodobieństwo zastania króla u W jest więc dwa razy większe niż zastania go u E, czyli wynosi 2/3 (67%).

Po przekształceniu powyższego mamy wzór na iloczyn zdarzeń zależnych:

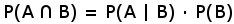
Sprawdźmy poprawność prawdopodobieństwo drugiego króla pod impasem gdy brakuje 5 kart, obliczonego w przykładzie 2 przy zastosowaniu kombinacji:

• A - król u W
• B - 2 karty u W. P(B)=34% (połowa układów 3-2 odczytana z tabeli podziału koloru
• A|B - król u W pod warunkiem, że są tam dwie karty. Obliczenie prawdopodobieństwa sprowadza się do policzenia układów z drugim królem (4 układy), a następnie podzielenia tego przez liczbę wszystkich możliwych układów dwukartowych u W. Tych układów jest 10 (kombinacje 2 z 5) - prawdopodobieństwo wynosi więc 4/10 (40%)
• A∩B - część wspólna A i B, czyli drugi król u W. Po podstawieniu do wzoru otrzymujemy P(A∩B)=40%*34%=14%

Zasada ograniczonego wyboru

Zapewne każdy spotkał się z tym pojęciem. Jest to zasada wynikająca z prawdopodobieństwa warunkowego właśnie. Załóżmy, że masz do wzięcia trzy lewy w poniższym układzie. Siedzisz na pozycji S i masz jeszcze jedno dojście do ręki.

Wygląda na to, że trzeba podwójnie zaimpasować piki. Jedna z dwóch figur pod impasem to 75%, natomiast impas kiera, a potem impas pika to tylko niecałe 63% (50%+50%*25%). Impasujemy więc, E bierze lewę damą i odwraca bokiem. Znów jesteś w ręce i postanowiłeś przemyśleć sprawę. Wygląda na to, że teraz zarówno impas króla pik jak i impas króla kier ma takie same szanse powodzenia. Co się stało? Ano nastąpiła właśnie sytuacja kiedy trzeba zastosować naszą zasadę ograniczonego wyboru. E mając tylko damę pik musiał nią zabić naszą dzisiątkę, a mając zarówno damę jak i króla mógł położyć zarówno damę jak i króla. Można załozyć, że przy obu figurach u E, tylko w połowie wypadków pojawi się dama. Innymi słowy po zabiciu figurą, maleje szansa, że W ma drugą z figur.

Spróbujmy policzyć prawdopodobieństwo posiadania przez E króla pik, po zabiciu pierwszej lewy damą. Zdarzenie król u E, zastępujemy innym: król u E jeśli E zabił damą.

• A - król u E
• B - E zabił damą. Jeśli zabił damą to wchodzą w grę dwa układy: D lub KD. Oba tak samo prawdopodobne, z tym , że w drugim dama pojawi się tylko w połowie wypadków. P(B)=50%+50%*50%=75%
• A∩B - część wspólna (obie figury u E). Prawdopodobieństwo tego to 1/4 - jeden z czterech możliwych układów (D, K, KD, nic)
• Prawdopodobieństwo, że E ma króla, jeśli zabił damą w pierwszej lewie: P(A|B)=P(A∩B)/P(B)=25%/75%=33%

Wynika z tego, że w omawianej sytuacji szansa powodzenia w przypadku drugiego impasu w pikach wynosi nie 50% ale 67%

W omawianym przypadku poczynione zostało założenie, że E mając obie figury doda damę w połowie przypadków. Losowe dodawanie figur w takim układzie jest optymalną strategią. Zauważ, że gdyby E dodawał z takiej konfiguracji zawsze króla, to szansa udania się powtórnego impasu byłaby stuprocentowa. Gdyby miał jednak zwyczaj zawsze dodawać damę, to faktycznie szansa na udanie się impasu pik jak i impasu kier byłaby taka sama.

Kolejny przykład zastosowania zasady ograniczonego wyboru to także już abecadło brydżowe

Optymalna rozgrywka takiego układu polega na zagraniu asem lub królem, a następnie jeśli od E spadnie figura - impasie dziesiątką. Wydawałoby się, że jest to sposób niewłaściwy, gdyż szansa na podział 2:2 to 40%, a szansa na singlową figurę - tylko 12%. Policzmy jednak dokładnie. Po spadnięciu na przykład waleta są możliwe tylko dw układy u E:

• singlowy walet - sznasa wg tabeli - 6%
• DW sec - gdyby nie zależało od pierwszej zrzutki, prawdopdobieństwo wyniosłoby wg tej samej tabeli - 7%

Liczymy prawdopodobieństwo warunkowe ze wzoru P(A|B)=P(A∩B)/P(B) gzie:

• A - DW sec
• B - spadł walet. Zdarzenie obejmuje układy z singlowym waletem i połowę układów z DW sec. Ponieważ te dwie sytuacje się wykluczają, prawdopodobieństwo jest zwykłą sumą: 6% + 7% / 2 = 9,5%
• P(A∩B)- część wspólna A i B czyli połowa układów z DW sec - 3,5%

Prawdopodobieństwo DW sec u E jeśli spadł od niego walet wynosi więc tylko: 3,5% / 9,5% = 37%. Impas jest więcej niż uzasadniony.

Sprawdźmy jeszcze jeden dosyć częsty przypadek:

Chcemy w takim kolorze wziąć wszystkie lewy. Na zagranego króla od E spada dziesiątka. Gramy blotkę, W dokłada blotkę - impasować czy grać górą?

Wchodzą w grę trzy układy u E: singlowa dziesiątka, dziesiątka z blotką i D10 sec, z pradopodobieństwami a priori odpowiednio: 3%, 11%, 3%. Tylko w ostatnim wypadku powinniśmy grać z góry, widać, że ta szansa jest wyraźnie mniejsza niż pozostałe. Sprawdźmy czy zmieni się coś po zrzuceniu dziesiątki w pierwszej lewie przez E:>

• A - D10 sec u E
• B - od E spada dziesiątka. E dorzuci dziesiątkę jeśli ma ją singlową i z D10 oraz w połowie przypadków 10x. P(B)= 3% + 5,5% + 3% = 11%
• P(A∩B) - prawdopodobieństwo, że E ma D10 sec i zrzuci dziesiątkę - 3%

Pradopodobieństwo warunkowe P(A|B) = 27%. Wynika z tego, że jeśli od E spadnie dziesiątka, szansa na impas jest dużo wyższa niż zagranie z góry.

© 2008 jafo